Charlas a cargo de:

• Dr. Jorge X. Velasco Hernández

  IM, UNAM

  Una perspectiva personal de las matemáticas aplicadas en México
• Dr. Víctor Alfonso Vicente Benitez

  IM, UNAM

  Hablando de la ecuación de Sturm-Liouville en forma de impedancia (y de las aventuras para resolverla)

  En muchos problemas de la física (como en acústica, propagación de ondas, y mecánica cuántica), aparece la necesidad de resolver ecuaciones diferenciales de primer orden con coeficientes variables. Una de tales ecuaciones es la ecuación de Sturm-Liouville en forma de impedancia (SLEIF). Sin embargo, en nuestra formación básica como estudiantes, pocas veces se nos enseñan métodos prácticos para la solución de los mismos, salvo para ciertos casos particulares.

  En esta plática, abordaremos dos métodos recientemente descubiertos, para la solución general de la SLEIF: el método de series de potencias del parámetro espectral (SPPS) y las representaciones en series de Neumann de funciones de Bessel esféricas (NSBF). Ambos métodos tienen la particularidad de que nos proporcionan representaciones analíticas de las soluciones, a partir de las cuales es posible deducir un método numérico para la construcción de las mismas.

  Mostraremos cómo deducir ambas representaciones, y su aplicación a la solución del problema de Dirichlet asociado a la SLEIF, mostrando algunos ejemplos que muestran la eficacia de dichos métodos, y platicando también un poco, de las preguntas, dificultades, y aventuras que surgen en el proceso de hacer investigación en análisis y ecuaciones diferenciales.

• M.C. Ruth Corona Moreno

  IM, UNAM

  Modelos para el estudio de enfermedades transmitidas por el medio ambiente

  La propagación de infecciones bacterianas es uno de los mayores problemas sanitarios a nivel mundial, debido a su facilidad de propagación a través del ambiente y al desarrollo de resistencia a antibióticos. Enfermedades como el cólera y la toxoplasmosis son transmitidas por bacterias que se propagan principalmente por medio de agua contaminada, que a pesar de la implementación de estrategias de sanitización no ha sido posible erradicar de ciertas regiones del mundo. Por otra parte, bacterias como la E.coli y la C. difficile son transmitidas durante estancias hospitalarias, principalmente por medio de objetos contaminados (fomites), y repercuten en el desarrollo de enfermedades crónicas en pacientes.

  En esta charla se expondrán dos propuestas de modelos compartimentales en EDO para estudiar la propagación de bacterias por medio del ambiente. En uno veremos que la existencia de ciertos parámetros, diferentes al número reproductivo básico, permiten caracterizar la dinámica de transmisión de bacterias por medio del ambiente, mostrando la existencia de bifurcaciones hacia atrás que producen múltiples estados de equilibrio, dependiendo de las condiciones iniciales del sistema. Por otra parte, el segundo modelo busca incorporar características de propagación de bacterias dentro de un ambiente hospitalario, incorporando la posibilidad de superinfección por contacto con fomites y por el mal suministro de tratamientos.

• Tishbe Pilarh Herrera Ramírez

  IM, UNAM

  Denguestim: un modelo matemático para estimar brotes de Dengue en la república mexicana. La dificultad al trabajar con datos reales.

  Para mejorar las medidas de control y prevención del dengue es importante comprender la dinámica de la enfermedad y su relación con las poblaciones de mosquitos. Resulta fundamental estudiar modelos matemáticos que comparen y tomen en cuenta que las bases de datos reportadas ignoran que existen casos que no presentan síntomas y que no llegan al sistema de salud. En esta charla, presentaremos un modelo que tiene en cuenta esta idea y estima la enfermedad que no se ve. El modelo que denominamos Denguestim es un modelo estocástico que permite estimar la cantidad de casos de las diferentes fases de la enfermedad DNG, DG y defunciones, y tiene en cuenta los tiempos de retraso tanto en el registro como en la confirmación de los casos positivos.

  En esta charla se hablará de modelos matemáticos que se construyen con los datos disponibles, de las implicaciones que hay que considerar al trabajar con datos reales, de algunas ventajas y dificultades que tiene el modelado desde esta perspectiva.

• Dr. Guillermo Ramírez Santiago

  IM, UNAM

  Un modelo de angiogénesis en la evolución de un tumor en la córnea de ratones y conejos

  La angiogénesis es el proceso mediante el cual se forman nuevos vasos sanguíneos a partir de los preexistentes. Este proceso es crucial en el crecimiento tumoral, debido a que vincula las fases de crecimiento avascular, generalmente inofensivo, con el crecimiento vascular, que puede ser potencialmente mortal. En esta plática presentaremos el análisis de un modelo cuantitativo de angiogénesis que incorpora los aspectos más importantes que dan lugar a los brotes capilares que emergen de un vaso sanguíneo como resultado de la migración de células endoteliales. Las células endoteliales responden a estímulos quimiotácticos y haptotácticos producidos por factores angiogénicos y a su interacción con la fibronectina presente en la matriz extracelular, respectivamente. La dinámica espacio-temporal del proceso angiogénico se describe mediante un sistema de ecuaciones de reacción-difusión. Los resultados obtenidos reproducen algunas de las características que se observan en la respuesta neovascular a la implantación de fragmentos de tumor en la córnea de un ratón y de un conejo.

• Dra. Marina Manea

  Centro de Geociencias, UNAM

  Secretos de los montes submarinos: Uso de la magia del modelado numérico para rastrear el calor y el movimiento del agua

  Un gran número de discontinuidades batimétricas marcan el fondo de los océanos. Entre estas características, los montes submarinos que sobresalen de la capa sedimentaria pueden desempeñar un papel fundamental en el establecimiento de un intercambio continuo de fluidos y calor entre la litosfera oceánica y el océano. Aquí les voy a presentar el resultado de modelado numérico con códigos de elementos finitos para calcular las distribuciones de flujo, temperatura y presión dentro de los montes submarinos. Resolvemos las ecuaciones acopladas de continuidad, la ecuación de Darcy y la ecuación de conservación de energía en 2D. Presentamos un modelo numérico axisimétrico adaptado a la geometría real del monte submarino llamado Grizzly Bare, ubicado en la placa oceánica de Juan de Fuca. El flujo de calor superficial muestra una buena correlación entre nuestros modelos y las observaciones in situ disponibles. En este trabajo, proporcionamos acceso abierto completo a códigos numéricos que buscan ser simples y fáciles de adaptar a una amplia gama de formas y tamaños de montes submarinos.

• Dr. Mario Santana Cibrián

  ENES-Juriquilla, UNAM

  Estimación en modelos dinámicos con métodos Markov Chain Monte Carlo

  Los modelos dinámicos, tanto deterministas como estocásticos, son ampliamente utilizados para describir fenómenos que evolucionan en el tiempo, como la propagación de enfermedades, la dinámica poblacional o el comportamiento de sistemas físicos y sociales. Sin embargo, la estimación de sus parámetros a partir de datos observacionales representa un desafío. En esta plática se abordará la estimación de parámetros en modelos dinámicos mediante métodos Markov Chain Monte Carlo (MCMC).

  Se presentarán los fundamentos de los métodos MCMC y su aplicación en contextos bayesianos, donde se busca aproximar distribuciones posteriores a partir de simulaciones. Se discutirán algoritmos clásicos como Metropolis-Hastings y Gibbs Sampling, así como variantes adaptativas y técnicas avanzadas para mejorar la eficiencia computacional y la convergencia de las cadenas.

  A través de ejemplos concretos se ilustrará cómo formular un modelo dinámico, establecer una estructura probabilística coherente y aplicar métodos MCMC para inferir parámetros clave.

• Dra. Dara Salcedo González

  UNDI-FC, UNAM

  Caracterización química de aerosoles atmosféricos
• Dr. Gerardo Hernández Dueñas

  IM, UNAM

  Modelación matemática de los efectos de aerosoles en la microfísica de nubes

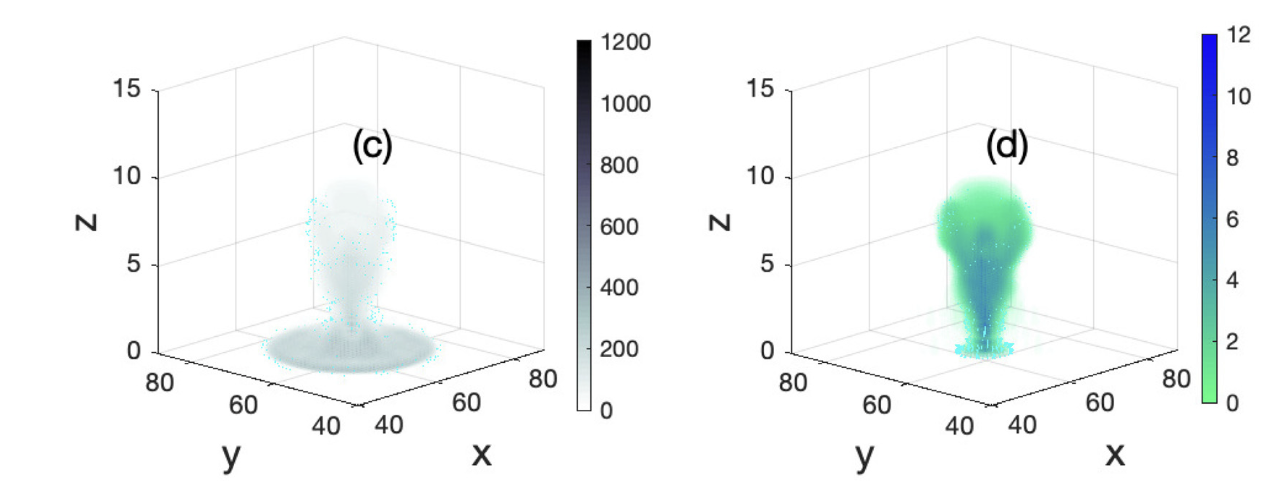
  Durante décadas, se ha estudiado cómo la contaminación atmosférica puede influir en la formación e intensidad de la lluvia. Estos estudios se han sustentado en datos experimentales, así como en los resultados numéricos de modelos matemáticos desarrollados con este fin. Dichos estudios han demostrado que el exceso de aerosoles en la atmósfera puede inhibir, reducir o incluso incrementar la precipitación. Este fenómeno es complejo y requiere de la parametrización de procesos físicos que ocurren en diversas escalas espaciales y temporales. En esta charla, presentaremos un modelo simplificado en 3D, basado en Ecuaciones Diferenciales Parciales, que permite parametrizar la convección turbulenta precipitante, incorporando el efecto de los núcleos de condensación en el proceso de formación de nubes. A través de diversas simulaciones, mostraremos cómo la concentración y distribución de estos núcleos influyen en la formación e intensidad de la lluvia. Este trabajo es realizado en colaboración con Olmo Guerrero Medina.